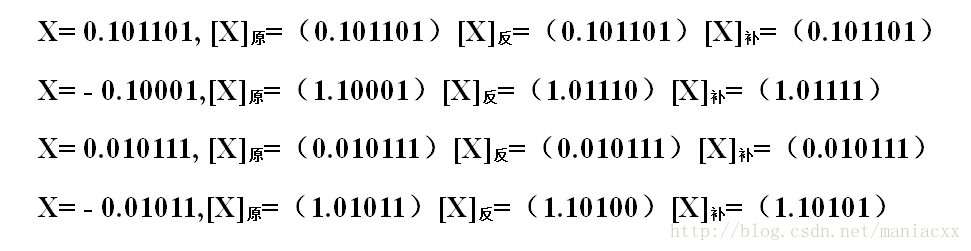1、填空题
1) 计数进位制转换
高进制转低进制:除k取余法
低进制转高进制:乘k取整法
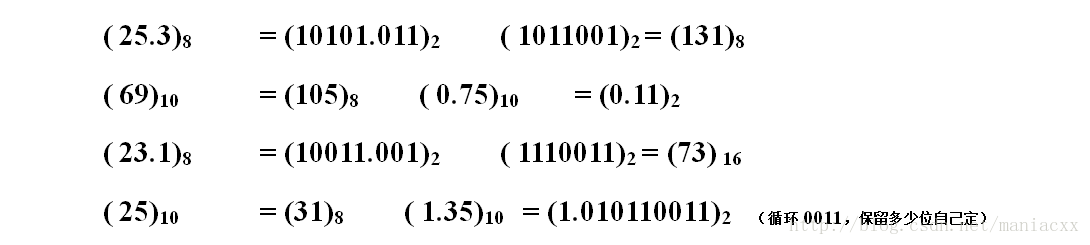
2) 符号数的编码表示
正数原,反,补一样
负数反码为原发除符号取反,补码为反码在最低位加1
最高位0表示正,1表示负校验法: (1) 奇偶校验码:可以验证传输过程是否产生了错误 1) 奇校验:为二进制添加一位校验码,使1的数量为奇数
2) 偶校验:为二进制添加一位校验码,使1的数量为偶数 (2) 海明码:传输过程中错一位概率大,通过海明码可以验证是哪位错了
在2的k次方位数上放校验码,例如传输三位的时候,在第一位和第二位放校验码,第三位存信息,利用第一位和第二位和第三位进行偶校验,若产生两位验证位为00,则正确,01是第1位错了,10是第二位错了,11是三位都错了,拓展海明码位数就能增加信息位位数,增强实用性
二进制按顺序排列第k位校验位管理对应二进制第k位为1的信息位
2.可靠性编码设计:设计一种含3位校验位的海明码方案,1)信息位与校验位的排列关系与交叉校验的编组表,2)校验位及校验和的生成函数。
3.可靠性编码设计:设计一种含7位信息位的奇校验编码方案,1)说明检错的原理,2)写出校验位及校验和的生成函数。
4.可靠性编码设计:设计一种含7位信息位的偶校验编码方案,1)说明检错的原理,2)写出校验位及校验和的生成函数。
5.用公式法化简函数并表示为与或式。
与或式:先与后或
或与式:先或后与
与非式:只有与非,无或
常用公式:
5-1
5-2
5-3
5-4
5-5
5-6
6.利用卡诺图法化简逻辑函数
最小项用m表示,最大项用M,d或D表示任意值 卡诺图中1表示最小项中的A,则表示最大项中的~A(A非)
1)表示为最简与或式
2)写出对应的最大项表达式,化简并表示为最简或与式
6-1
6-2
6-3
7.逻辑函数变换
转与非方法:加两个非号不影响值,打开里面的非号
7-1
7-2
转或非方法:(1)加法分配律转化为或与式,再加双非号,打开内部非号 (2)转发为与非式后利用最大项最小项特点化为或与式,再加两个非号,打开内部非号
7-3
7-4
验证传化成的最大项与最小项答案可通过卡诺图,需注意最小项中A表示1,
A表示0,最大项中A表示0,A表示1
转化为最小项方法:补项
7-5
转化为最大项方法:加法分配率加补项
7-6

二进制全加器设计

二进制全减器设计

设计一种2-4译码器,并拓展为3-8译码器

设计一种2-4译码器,并拓展为4-16译码器
第一问用10题图中(1)(2)(3)可解
第二问

利用3-8译码器实现逻辑函数

利用3-8译码器实现逻辑函数

利用一种4-16译码器实现逻辑函数

利用一种2-4译码器实现4选1的多路选择器,并扩展为8选1的多路选择器

利用一种4选1的多路选择器实现逻辑函数

利用一种2-4译码器实现4路的多路分配器,并扩展为8路分配器

利用D型触发器设计同步检测器

利用D型触发器设计一个2位的二进制同步可逆计数器

多功能同步移位寄存器