KJHの博客

记录&回忆

0%

STL红黑树

发表于 更新于 分类于
本文字数： 12k 阅读时长 ≈ 11 分钟

红黑树概述

历史上 AVL 树流行的另一变种是红黑树（red-black tree）。对红黑树的操作能保证在最坏情况下动态几何操作的时间为 O(logN) 。之前介绍过AVL 树，该树都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。但 RB-Tree 出来之后，便很少有应用场合用到 AVL 。

这里在探索STL源码时学习红黑树的，由于STL中的关联式容器默认的底层实现都是红黑树，以及 Linux 内核中包括进程队列等结构也是基于红黑树的。所以有必要掌握红黑树的实现原理和源码实现。

红黑树是二叉查找树，但在每个节点上增加了一位存储位表示该节点的颜色，具体可以是 RED 或 BLACK。通过对任一条从根到叶子的路径上各节点着色方式的限制，红黑树确保了没有一条路径会比其他路径长到两倍，因而基本上是平衡的。它所追求的的是局部平衡而不是AVL树中的非常严格的平衡。

红黑树在二叉查找树的基础上还必须满足以下着色规则：

  1. 每个节点不是红色就是黑色
  2. 根节点为黑色
  3. 如果节点为红，其子节点必须为黑（一条路径上不能出现连续的两个红色节点）
  4. 任一节点至NULL（树尾端）的任何路径，所含之黑节点数必须相同

根据规则4，新增节点必须为红；根据规则3，新增节点之父点必须为黑。当新节点根据二叉查找树的规则（键值大小）到达其插入点，却未能符合上述条件，就必须调整颜色并旋转树形。AVL 树插入节点后如果不满足其平衡条件，需要旋转树形。红黑树并不是基于 AVL 树的，它是在二叉查找树的基础上。

那么红黑树的基本平衡又是如何保证的呢？红黑树的着色法则，根据上面的规则，一条路径上不能出现连续的两个红色节点，必须有黑色节点间隔开来，然后红黑树的每条路径中所含黑色节点的数目必须相同，这样就限制每条路径之间的高度差，从而达到接近平衡的目的。

\插入节点**

同 AVL 树，红黑树的插入也要考虑以下几种情况，然后兼顾上面的着色法则。所有待插入节点初始着色为红色，最后将根节点重新设置为黑色。

1、空树

这是最简单的一种形式，直接添加，着色为黑色（规则2）

2、仅存在根节点（黑色），或待插入节点 X 的父节点 P 为黑色

直接添加即可，无需任何旋转和调整颜色。这种情况下，直接添加满足所有的着色法则，不用理会其叔节点的特征。

3、待插入节点 X 的父节点 P 为红色，且该父节点 P 为X 祖父节点G 的左儿子

这种情况下，又分为几种情况：

3.1、X 的叔节点 S 为红色，（X 的叔节点就是 X 的祖父节点的右儿子）

此时存在红- 红的情况，父子节点同时为红色，不满足着色法则3，需要作出调整。

调整策略就是：将X 节点的父节点和叔节点着黑色，将其祖父节点着红色，这样该局部满足着色法则，但是尚不清楚其曾祖父GG节点的颜色，如果GG为红色，由于G也为红色，这样就不满足着色法则3，仍需要调整；如果GG为黑色就不需要调整了，这里的调整策略便是向上迭代调整，就是向上更换当前位置（将原当前位置X，设置为X的祖父节点G），再进行同等判断调整。如下图：

img

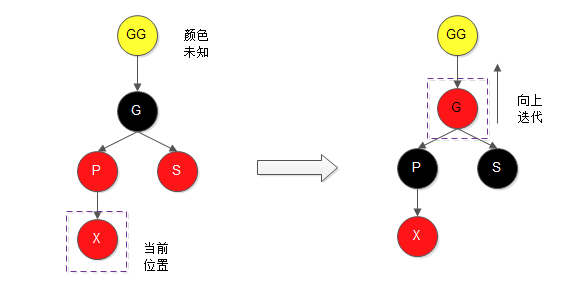
3.2、X 的叔节点 S 为黑色（NULL认为是黑色节点）

红黑树还有个规则就是NULL节点一律看作是黑节点，如某节点K 的右儿子不存在，即该右儿子看作是黑色节点，这个不影响着色法则。

叔节点S 为黑，这样就需要通过旋转和改变颜色来调整了，通过之前的 AVL 树，我们知道外侧插入和内侧插入的旋转不一样，外侧插入（这里的左左）只需单旋转，而内侧插入（左右）则需要双旋转。

3.2.1、先看看外侧插入，即待插入节点X 为其父节点的左儿子

这种情况下，需要进行单旋转然后调整颜色。关于外侧插入的旋转已经在AVL树中介绍，这里是相似的，不再赘述。实现细节看图便知

img

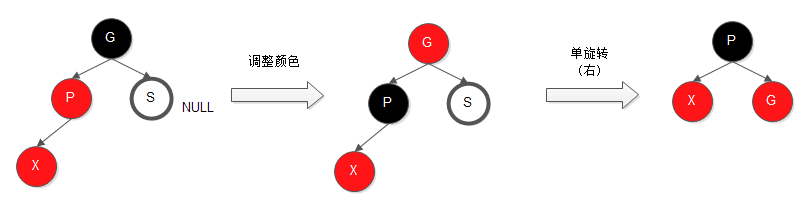
调整前后局部根节点还是黑色，也就是这种情况下只需要局部调整颜色然后单旋转即可，不需要向上迭代

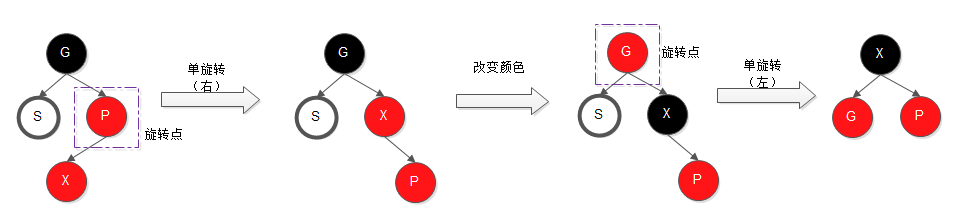
3.2.2、内侧插入，即待插入节点X 为其父节点的右儿子

该情况下，需要先进行左旋转，然后调整颜色，然后再次进行右旋转即可，前后局部根节点依旧为黑色节点，同样不需要考虑上一层的红-红问题，实现细节如下图：

img

上述第3点考虑的是待插入节点的父节点 P 为X 祖父节点G 的左儿子的情况，其作为右儿子也是类似的操作，差别在于旋转的先后顺序上，同AVL树的旋转调整。这里也顺便贴出来，见第4点

4、待插入节点 X 的父节点 P 为红色，且该父节点 P 为X 祖父节点G 的右儿子

同样分为以下几种情况，由于与第3点是对称性结构，这里就简单的贴图说明：

4.1、X 的叔节点 S 为红色，（X 的叔节点就是 X 的祖父节点的左儿子）

具体说明参见3.1。同样需要解决红-红（父子节点同时为红色）的问题，调整位置向上迭代判断调整

img

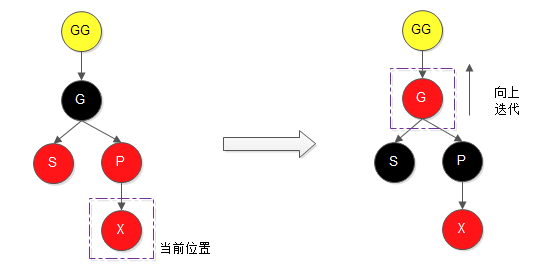
4.2、X 的叔节点 S 为黑色（NULL认为是黑色节点）

也是需要考虑外侧插入和内侧插入的情况

4.2.1、外侧插入，即待插入节点X 为其父节点的右儿子

img

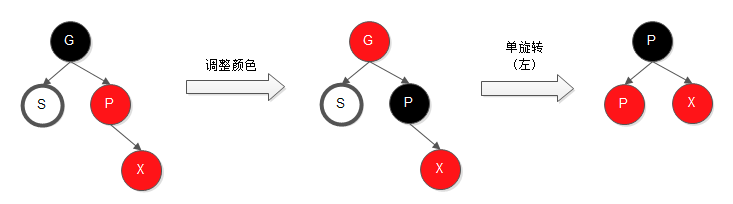
4.2.2、内侧插入，即待插入节点X 为其父节点的左儿子

img

以上便是红黑树插入节点的所有情况。

下面我们通过STL的源码来剖析上述过程：

先看看两个关键函数：\左旋转和右旋转**

左旋转*\*：**
****

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*左旋转*/
inline void
__rb_tree_rotate_left(__rb_tree_node_base* x, __r_node_base*& root)
{
	//X为旋转点
	__rb_tree_node_base* y = x->right;//令Y为旋转点的右子节点

	x->right = y->left;//X的右子节点指向Y的左子节点
	if (y->left != 0)
		y->left->parent = x;//如果Y有左儿子，则其左儿子的父节点设置为X
	y->parent = x->parent;//Y的父节点设为X的父节点
	if (x == root)
		root = y;//如果X为根节点，则将Y设为根节点
	else if (x == x->parent->left)
		x->parent->left = y;//如果X为其父节点的左儿子，则将X的父节点的左儿子设为Y
	else
		x->parent->right = y;//如果X为右儿子，则将其父节点的右儿子设为Y
	y->left = x;//Y的左儿子设为X
	x->parent = y;//X的父节点设为Y
}

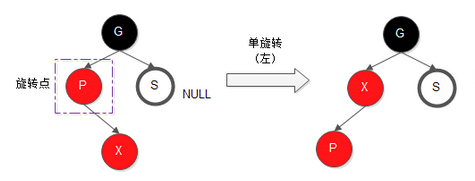
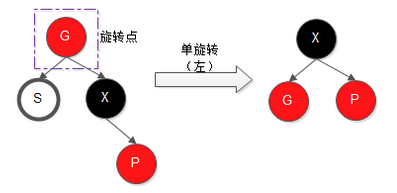
其旋转过程参见下图：

img & img

右旋转：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*右旋转，必须将所有父子关系转接过来*/
inline void
__rb_tree_rotate_right(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{  
	//X为旋转点
	__rb_tree_node_base* y = x->left;//令Y为旋转点的左子节点
	x->left = y->right;//X的右子节点指向Y的右子节点
	if (y->right != 0)
		y->right->parent = x;//如果Y有右儿子，则其右儿子的父节点设置为X
	y->parent = x->parent;//Y的父节点设为X的父节点
	/*将Y完全替代X的地位，将X的所有父子关系转接过来*/
	if (x == root)
		root = y;//如果X为根节点，则将Y设为根节点
	else if (x == x->parent->right)
		x->parent->right = y;//如果X为其父节点的右儿子，则将X的父节点的右儿子设为Y
	else
		x->parent->left = y;//如果X为左儿子，则将其父节点的左儿子设为Y
	y->right = x;//Y的右儿子设为X
	x->parent = y;//X的父节点设为Y
}

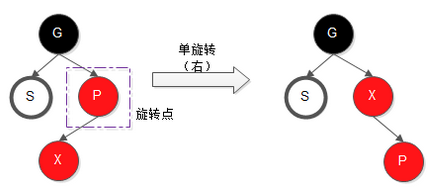
旋转示意图如下

img & img

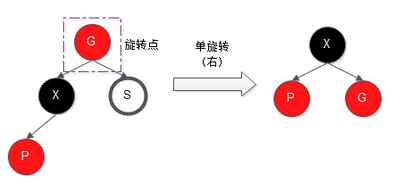
有了前面的旋转函数，接下来来看看STL中红黑树插入节点后的\平衡调整函数**：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
/*调整红黑树，旋转以及改变颜色*/
inline void
__rb_tree_rebalance(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
	//X为新插入节点
	x->color = __rb_tree_red;//新插入节点初始为红色
	while (x != root && x->parent->color == __rb_tree_red)//父节点为红
	{
		if (x->parent == x->parent->parent->left)//X的父节点为其祖父节点的左儿子
		{
			__rb_tree_node_base* y = x->parent->parent->right;//Y指定为X的叔节点
			if (y && y->color == __rb_tree_red)//如果X的叔节点存在且为红色
			{
				/*调整颜色，需要向上迭代，直至满足着色法则第3点（不能红-红）*/
				x->parent->color = __rb_tree_black;//X的父节点着黑色
				y->color = __rb_tree_black;//X的叔节点Y着黑色
				x->parent->parent->color = __rb_tree_red;//X的祖父节点着红色
				x = x->parent->parent;//调整位置，将当前位置重置为X的祖父节点，开始上层迭代调整

			}
			else//X的叔节点不存在或者为黑色
			{
				if (x == x->parent->right)//X为右儿子，即内侧插入（左右）
				{
					x = x->parent;//设置旋转点为X的父节点，不影响后面if外X的值
					__rb_tree_rotate_left(x, root);//以X(实际为原X的父节点)为旋转点左旋转
				}
				//因为上面X的赋值在随后的左旋转已经彻底转换了父子关系，所以后面的X还是指向新插入节点位置(不是值)
				x->parent->color = __rb_tree_black;//将X的父节点着黑色
				x->parent->parent->color = __rb_tree_red;//X的祖父节点
				__rb_tree_rotate_right(x->parent->parent, root);//以X的祖父节点为旋转点右旋转
			}
		}
		else//X的父节点为其祖父节点的右儿子
		{
			__rb_tree_node_base* y = x->parent->parent->left;//Y指定为X的叔节点
			if (y && y->color == __rb_tree_red)//如果X的叔节点存在且为红色
			{
				/*调整颜色，并向上迭代判断调整*/
				x->parent->color = __rb_tree_black;
				y->color = __rb_tree_black;
				x->parent->parent->color = __rb_tree_red;
				x = x->parent->parent;//调整位置
			}
			else
			{
				if (x == x->parent->left)
				{
					x = x->parent;
					__rb_tree_rotate_right(x, root);//以X(原X的父节点)为旋转点，右旋转
				}
				x->parent->color = __rb_tree_black;
				x->parent->parent->color = __rb_tree_red;
				__rb_tree_rotate_left(x->parent->parent, root);//以X的祖父节点为旋转点进行左旋转
			}
		}
	}//end while
	root->color = __rb_tree_black;//最后将根节点着色为黑色
}

有了前面的介绍，相信不难理解这个程序。上面便是红黑树插入节点后的核心部分程序

再来看看红黑树的插入函数，在了解红黑树的插入操作之前，有必要先了解红黑树的数据结构以及构造和内存管理

先看看\红黑树的节点结构**

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/*红黑树rb_tree 的节点结构*/
struct __rb_tree_node_base
{
	typedef __rb_tree_color_type color_type;
	typedef __rb_tree_node_base* base_ptr;
	color_type color;
	base_ptr parent;
	base_ptr left;
	base_ptr right;
	/*求取X节点以下的最小值(小于等于X的最小值)*/
	static base_ptr minimum(base_ptr x)
	{
		while (x->left != 0) x = x->left;
		return x;
	}
	/*求取X节点以下的最大值（大于等于X的最大值）*/
	static base_ptr maximum(base_ptr x)
	{
		while (x->right != 0) x = x->right;
		return x;
	}
};

接下来红黑树rb_tree 的类体结构，由于比较大，这里只摘取相关部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
template <class Key, class Value, class KeyOfValue, class Compare,
class Alloc = alloc>
class rb_tree {
protected:
	/*typedef 数据类型*/
	typedef void* void_pointer;
	typedef __rb_tree_node_base* base_ptr;
	typedef __rb_tree_node<Value> rb_tree_node;
	typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator;
	typedef __rb_tree_color_type color_type;
public:
	……
	typedef rb_tree_node* link_type;
protected:
	/*分配节点空间*/
	link_type get_node() { return rb_tree_node_allocator::allocate(); }
	/*释放节点空间*/
	void put_node(link_type p) { rb_tree_node_allocator::deallocate(p); }
	/*创建一个节点*/
	link_type create_node(const value_type& x) 
	{
		link_type tmp = get_node();//获取空间
        //……省略捕获异常  
		construct(&tmp->value_field, x);//构造内容
	}
	link_type clone_node(link_type x)//复制一个节点（值和颜色）
	{
		link_type tmp = create_node(x->value_field);
		tmp->color = x->color;
		tmp->left = 0;
		tmp->right = 0;
		return tmp;
	}
	void destroy_node(link_type p)//删除节点
	{
		destroy(&p->value_field);//析构内容
		put_node(p);//释放节点空间
	}
protected:
	size_type node_count; // keeps track of size of tree
	link_type header;//这是实现上的一个技巧，该类没有单独指定根节点，header->parent就是指向根节点
	Compare key_compare;
	/*以下三个函数用来方便取得 header 的成员*/
	link_type& root() const { return (link_type&)header->parent; }//树的根节点
	link_type& leftmost() const { return (link_type&)header->left; }//树的最小节点
	link_type& rightmost() const { return (link_type&)header->right; }//树的最大节点
	/*以下六个函数用来方便取得节点 X 的成员*/
	static link_type& left(link_type x) { return (link_type&)(x->left); }
	static link_type& right(link_type x) { return (link_type&)(x->right); }
	static link_type& parent(link_type x) { return (link_type&)(x->parent); }
	static reference value(link_type x) { return x->value_field; }
	static const Key& key(link_type x) { return KeyOfValue()(value(x)); }
	static color_type& color(link_type x) { return (color_type&)(x->color); }
	/*省略类型base_ptr的同类函数，功能一样*/
	/*求取极小值*/
	static link_type minimum(link_type x) {
		return (link_type)__rb_tree_node_base::minimum(x);
	}

	/*求取极大值*/
	static link_type maximum(link_type x) {
		return (link_type)__rb_tree_node_base::maximum(x);
	}
private:
	iterator __insert(base_ptr x, base_ptr y, const value_type& v);
	link_type __copy(link_type x, link_type p);
	void __erase(link_type x);
	/*下面这个函数需要说明一下*/
	void init() {
		header = get_node();//产生一个节点空间，让 header 指向它
		color(header) = __rb_tree_red; //令header 为红色，用于区分root
		root() = 0;//header->parent = 0
		leftmost() = header;//令header 的左儿子为自己
		rightmost() = header;//令header 的右儿子为自己
	}
public:
	// allocation/deallocation
	rb_tree(const Compare& comp = Compare())
		: node_count(0), key_compare(comp) {
		init();
	}
	/*拷贝构造函数*/
	rb_tree(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x)
		: node_count(0), key_compare(x.key_compare) 
	{
		header = get_node();
		color(header) = __rb_tree_red;
		if (x.root() == 0)//拷贝空树，仅存在header
		{
			/*设置 header*/
			root() = 0;
			leftmost() = header;
			rightmost() = header;
		}
		else 
		{
			/*树结构拷贝*/
			root() = __copy(x.root(), header);//x.root()就是树x的根节点
			//省略异常处理部分
			/*设置最大值和最小值
			header 的父节点指向根节点，然后左子节点指向最小节点，右子结点指向最大节点*/
			leftmost() = minimum(root());//不为空树，root()则返回根节点(header的父节点)
			rightmost() = maximum(root());
		}
		node_count = x.node_count;
	}
	/*析构函数*/
	~rb_tree() 
	{
		clear();
		put_node(header);
	}
	/*赋值构造函数*/
	rb_tree<Key, Value, KeyOfValue, Compare, Alloc>&
		operator=(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x);
    ……
};

这里对上面的 header 节点说明一下，树状结构的各种操作，最需注意的就是边界情况的发生，也就是走到根节点是要有特殊的处理，这里STL 特别为根节点再设计了一个父节点 header，而当插入节点后，header 的父节点指向根节点，其左子节点指向树的最小节点，右子结点指向树的最大节点。类似于链表的表头，这里也多了个头节点不实际存储数据，为管理而存在。

​ img

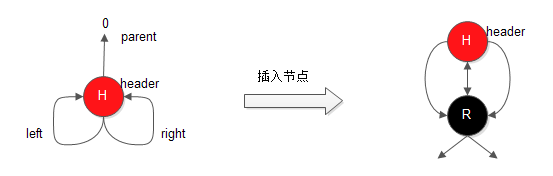
也就是在一棵非空红黑树中，header->parent 就是指的该树的根节点，header->left 就是指该树的最小节点，header->right 就是指该树的最大节点。

有了前面的了解，接下来看看红黑树的插入操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/*插入节点：节点键值不允许重复，若重复则插入无效
返回值是个pair，第一元素是个 rb_tree 迭代器，指向新增节点*/
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
pair<rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator, bool>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_unique(const Value& v)
{	
    link_type y = header;//y为根节点的父节点
	link_type x = root();//x为根节点
	bool comp = true
	while (x != 0)//从根节点开始，往下寻找适当的插入点
	{
		//二叉查找树特性插入
		y = x;
		comp = key_compare(KeyOfValue()(v), key(x));//比较新增值v 和x节点的键值
		x = comp ? left(x) : right(x);//v遇"大"则往左，遇"小或等于"往右
	}//while内单次每次运行结束，y总为x的父节点
	iterator j = iterator(y);//此时y节点必为叶子节点
	if (comp)//v小于比较值，将插入左侧
	{	
		if (j == begin())//begin()实际就是header->left，也就是树的最左节点
			return pair<iterator, bool>(__insert(x, y, v), true);//转入实际插入函数__insert()
		else//如果插入点之父节点不为最左节点
			--j;//调整j，--重载，调用decrement()，即找到比当前节点小的最大节点
		//与此同时还有++重载，调用increment()，找到比当前节点大的最小节点
	}
	if (key_compare(key(j.node), KeyOfValue()(v)))//遇"小"将插入右侧(v值大)
		return pair<iterator, bool>(__insert(x, y, v), true);
	/*以上，x为新插入点位置，y为插入点之父节点，v为键值*/
	return pair<iterator, bool>(j, false);//存在重复键值就不插入
}
/*插入节点：节点键值允许重复
返回值是一个 rb_tree 迭代器，指向新增节点*/
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_equal(const Value& v)
{
	link_type y = header;//y为根节点的父节点
	link_type x = root(); //x为根节点
	while (x != 0)//从根节点开始，往下寻找适当的插入点
	{
		y = x;
		//直接找到合适位置，无需考虑键值是否重复
		x = key_compare(KeyOfValue()(v), key(x)) ? left(x) : right(x);
	}
	return __insert(x, y, v);

}

从上面可知，真正的插入操作是\__insert()**

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/*x为新增节点位置，y为新增节点的父节点，v为新增节点的键值*/
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::
__insert(base_ptr x_, base_ptr y_, const Value& v) {
	link_type x = (link_type)x_;
	link_type y = (link_type)y_;
	link_type z;
	if (y == header || x != 0 || key_compare(KeyOfValue()(v), key(y)))
	{
		z = create_node(v);//为新节点配置空间
		left(y) = z;                // also makes leftmost() = z when y == header
		if (y == header)//如果y为头节点，也就是空树第一次插入节点
		{
			root() = z;//z为根节点，与header节点互为父节点
			rightmost() = z;//树的最大节点
		}
		else if (y == leftmost())//如果y为最左节点
			leftmost() = z;//修正最小节点
	}
	else//上面三种全不满足，即插入键值大于插入点的父节点，右侧插入
	{
		z = create_node(v);
		right(y) = z;//使新节点成为插入点的父节点y的右子结点
		if (y == rightmost())
			rightmost() = z;          // maintain rightmost() pointing to max node
	}
	//设置新增节点z的关系
	parent(z) = y;
	left(z) = 0;
	right(z) = 0;
	//平衡红黑树
	__rb_tree_rebalance(z, header->parent);
	++node_count;//节点数累加
	return iterator(z);//返回迭代器，指向新增节点

}

以上就是红黑树的整个节点插入操作过程